I’m a software engineering imposter. I know just enough to get by to get stuff done, but I’m not what I’d consider a software engineer with much of (any) theoretical underpinnings.
So I bought The Imposter’s Handbook by Rob Conery and get cracking. First up, Big O notation.
Polynomial Time a.k.a. “Easy”
The very first part of the book gets us thinking about how to…think about…complexity.
There’s a great example of six people trying to decide where to go for dinner. Each person has their own idea of what should happen, and they need to listen to the other five people. It might look like this:
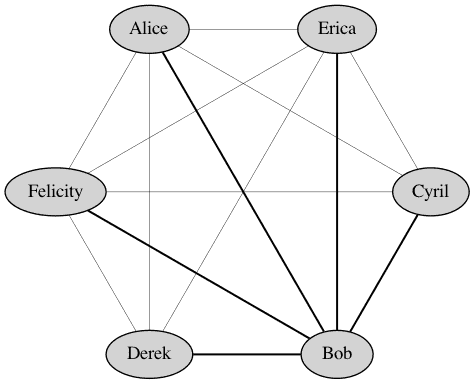
Six people with opinions about dinner
Which is to say, our 6 people each have an opinion about dinner and they get the opinion from the other 5.
Bob has to get 5 opinions in addition to his own; as do the other folks.
That’s $6\times6$, which is quadratic, or more generically $n^2$.
$n$ |
$n^2$ |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
So complexity is $O(n^2)$. Adding one element increases the time taken $T$ quadratically.
But it’s still $P$ time because the calculation is polynomial, i.e., multiplication, subtraction, addition, and non-negative integer exponents only.
Yes, it gets bad with bigger numbers in this case, but it’s manageable.
Exponential Time, a.k.a. “Hard”
As Conery points out, it’s not that simple.
In the first case, we have 6 people and $6^2$ options.
But in terms of making a final decision, each person has to consider the decisions of each of the other people.
Bob’s decision takes into account the decisions of each of the other 5 people. Erica’s decision takes Bob’s decision about where to go to dinner into account and the other 4 people before making her decision.
It’s exponential or “in EXP time”: $T = O(2^n)$.
$n$ |
$2^n$ |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
So if you had a collection of, say, 20 people then you’re looking at $T = 2^{20} = 1,048,576$.
To be continued…
I’m just capturing a few things I’m learning here, expect more over time. This may be better a as a Today I Learned. I may do that.